人工智能 ｜ 02 数字会说话

上文说到，人工智能在诞生的初期就形成了符号主义学派。他们认为，既然知识可以用各种各样的符号来表示，发现新的知识的本质就是符号之间的转化。

如果经由机器遍历完成所有合法的转化，那么我们就可以机械式的穷尽世间所有的知识，如此就可实现“人工智能”。

但是问题也随之而来了，“合法转化”中的“合法”所要符合的“法则”从何而来呢？

显然，符号之间的转化“法则”也是一种知识。可是这些“更高一层”的知识也可以通过遍历得到吗？

1931年数学家哥德尔提出了“不完备定理”，证明了这是不可能完成的任务。

那人工智能的出路在哪里呢？答案也许就藏在数字里。

模式识别

让我们来看这样一道简单的小学数学题。

不要想的太复杂，答案就是你心中的那个数字“6”，这组数字都是十以下的偶数。当然，在高中数学中，这也是一个等差数列。

题目看似很简单，但寓意非常深刻。

因为题目中并没有任何一个字说明这是一组偶数，或者这是一个等差数列。我们仅仅通过观察和直觉就识别了其中潜在的“模式”，并利用“模式”完成了“推理”。

如果我们面对的数字是来自于对真实世界的测量，那他们的内在模式不就是“知识”吗？！

原来知识就藏在数字里！

这个思路颠覆了以往科学研究的顺序：与其先提出假设，再用实验数据验证假设；不如先做实验收集数据，再识别数据中的特定模式，从而总结为知识。

这就是所谓的“模式识别”。

不过通过模式识别得到的“知识”也会有一些弊端，因为其经常看起来莫名其妙，无法理解。

对此，薛定谔表示有话想说。他通过总结量子现象提出了薛定谔方程和波函数理论，尽管可以非常好的进行预测，但实在与我们宏观世界的生活经验差距太大，让人无法理解。

甚至薛定谔本人都无法真正的理解方程的含义，为了让大众能同理到他的困惑，薛定谔还提出了那只著名的“既生又死”的猫。

不过理不理解呐，也没那么重要。知识嘛，能用就行。

联结主义

薛定谔终归还是幸运的，至少他给出了一个非常简洁的方程。（这也许说明了世界的本质很简单）。

但是很多其它的问题，就无法使用简单的方程来描述我们发现的模式，比如预测股票的涨跌，就涉及到非常多复杂的因素，如当前的股价、过去的走势、标的公司的股份组成和经营状况、金融环境与周期、国家的政策、国际上的经济形势等等。

每一个因素都可能与其它的因素之间蕴含着千丝万缕的联系，各种因素结合起来，最终影响了股价的走势。

既然使用单个方程难以描述其中的模式，数学家们想到了一个办法，就是使用一组相互联结的方程来“拟合”。

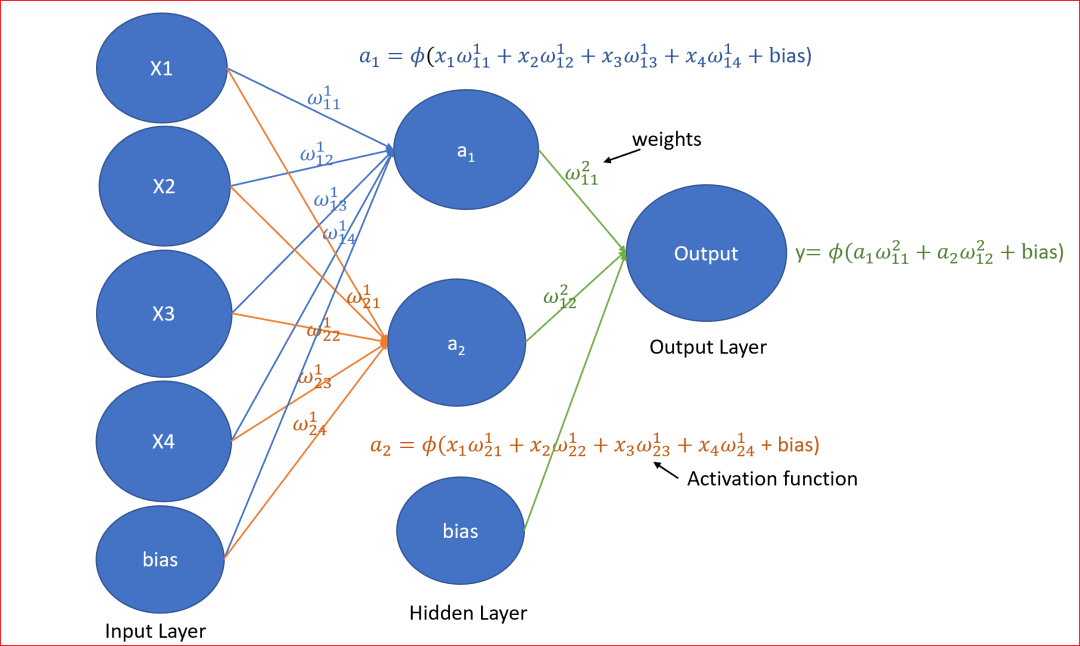
所谓“拟合”是说，这组方程描述的可能不是真相，但是其与实验和观测数据相符，我们就用这组方程来“模拟”真相。

这就诞生了人工智能的另外一个学派——“联结主义”。

如果我们暂时忽略具体方程，而只看他们形成的结构，会发现它无论是形态还是功能，它都神似人类中枢神经——大脑，于是命名为“神经网络”。

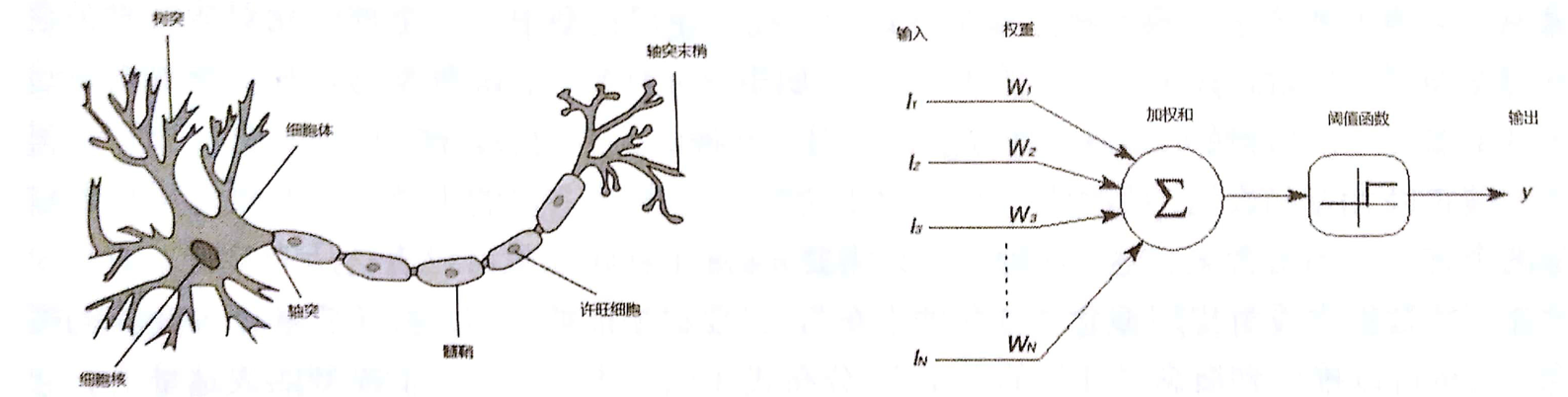
联结主义和神经网络是今天人工智能技术的主流，我们也会在接下来的文章中，使用大量的篇幅来讨论神经网络是如何构建出来的。

在此之前，为了避免被大量的抽象数字包围，我们还需要先了解一下名为“数据可视化”的重要方法。

数据可视化

数据是人类对客观世界的记录。

数据的形式也许是数字，也许是文字，甚至还有可能是图像、视频什么的，但在计算机里他们通通会被转化为数字。可以认为，数据就是被赋予了意义的数字。

比如身高170cm，体重65kg就是一组关于某人身体情况的基本数据，这里的170和65都有着特定的实际含义，分别代表着身高和体重。

计算机只关心数字本身，这组数据会被抽象为类似[170,65]这样形式，称之为“长度为2的数组”，或者在数学中称其为“2维向量”。

vector = [170, 65] # 2维向量

如果我们看到另外一个向量[185,76]，也能很容易的知道这是一位身高185cm，体重76kg的朋友。

我们还可以使用“2维数组”或“2阶向量”同时表示多条数据，看起来将会像这样：

# 每行表示一个人的数据
vectors = [[170, 65], 
           [185,  76]]

或者这样：

# 每列表示一个人的数据
vectors = [[170, 185], 
           [65,  76]]

这两种写法互为转置，在代码中可以很容易的转化，所以使用那种都可以，取决于应用场景。

下面的向量中存储了10个人的数据，那么请问哪位最“胖”？

vectors = [[170, 185, 183, 164, 177, 159, 182, 176, 168, 173],
           [65,  76,  80,  85,  65,  66,  70,  81,  69,  69]]

可以把向量画到坐标系中：

因为x轴为体重，y轴为身高，所以越靠近右下角的向量就越“胖”，结果非常的直观。

这里用到的画图库为matplotlib（需要单独安装），代码如下：

import matplotlib.pyplot as plt
# 数据向量
vectors = [[170, 185, 183, 164, 177, 159, 182, 176, 168, 173],
           [65,  76,  80,  85,  65,  66,  70,  81,  69,  69]]
# 绘制散点图
plt.scatter(vectors[1], vectors[0])
# 显示图像
plt.show()

这就是数据可视化，可以帮助我们通过视觉更好的理解数据背后的含义。

我将本专栏所有的代码托管在gitee上了，你可以点击这个链接，或到gitee.com上搜索弦五 人工智能，查看和获取本课程的全部代码。