人工智能 | 03 破开迷雾,回归本真
发现数据中隐藏的知识就像是拨开一团捉摸不定的迷雾,顺着些许线索回归真正的道路。

上文说到,联结主义是今天人工智能领域最主流的实现方式。
相比于“符号主义”将知识理解为符号,在“联结主义”中,知识是一组方程(函数),它们之间互相关联,形成一个类似于“大脑”的结构,所以亦称作神经网络。

和人类大脑的机制非常相似,一个神经网络在刚诞生的时候,它也是一张白纸,什么知识都没有,需要通过后天的学习,才能掌握知识。

可是神经网络本质上只是一些方程啊?方程也会学习吗?
为了理解这个问题,让我们从最简单的一元一次方程开始聊起。
方程中的参数
一个典型的一元一次方程,如下所示:
$$ y=ax+b $$其中x是自变量,y是因变量,a和b是方程的参数。
通常情况下,我们会很关注方程中的x和y,比如在求解方程的解时等。但在这里,我们将更加关注参数部分。
参数很有用,不同的参数决定了方程的功能和效果。
这就像使用洗衣机的时候,我们虽然目的是将衣服洗干净,但为此我们需要首先在洗衣机面板上设定好合适的参数,比如时长、水量、转速等等,不同的参数会影响洗衣的效果。

方程的参数正决定了它所描述的规律。比如在这个猜数字的题中,我们就可以使用$y=2x-2$来描述,这时参数$a=2$,参数$b=-2$。
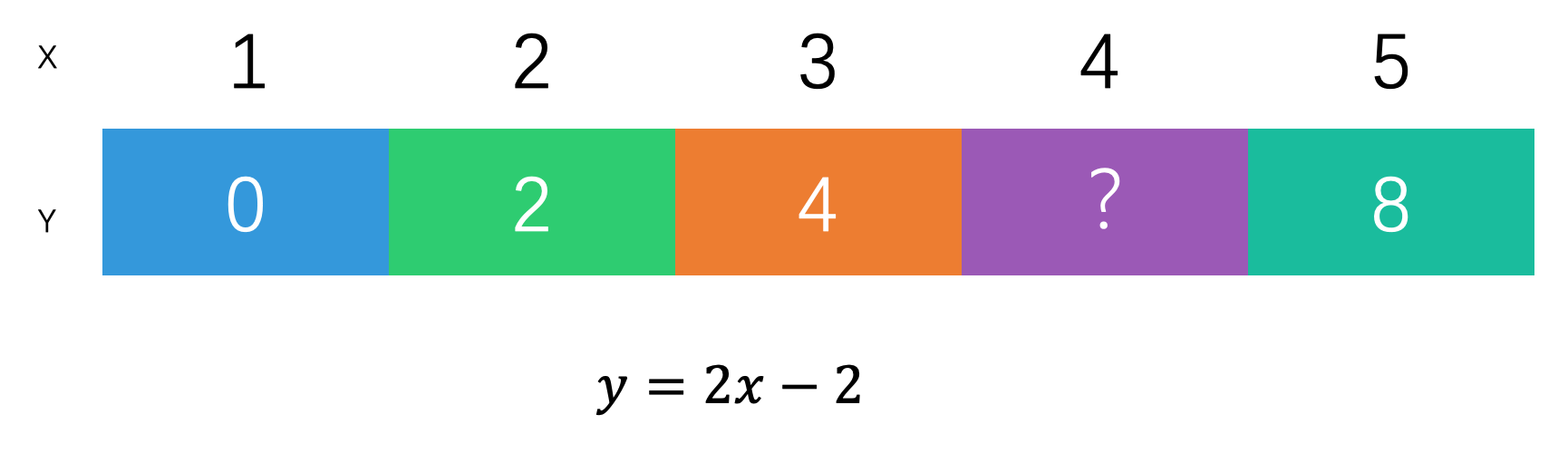
有了这个方程,我们就可以预测出这个数列中任意一位的数字,也就意味着掌握了知识。
使用可视化的方法在平面直角坐标系中绘制出一元一次方程,它将被表示为一条直线,这时可以更加直观的看到不同的参数对直线形态的影响。
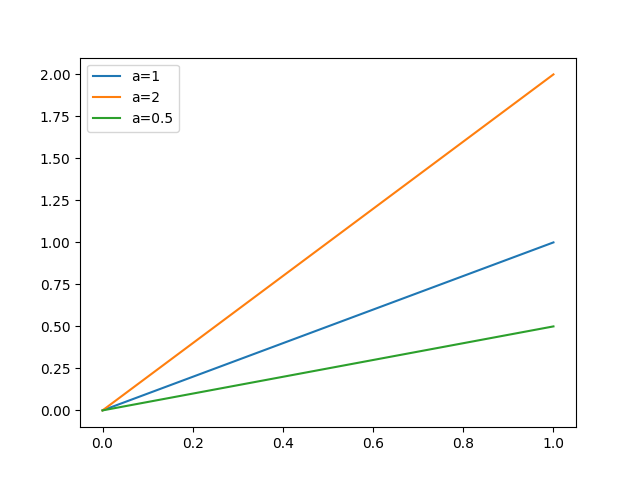
神经网络学习的本质,就是在寻找方程的最佳参数,使其尽可能最拟合数据的真实规律,这个过程又称作回归。
特别的,一元一次方程在坐标系中表现为一条直线,因此针对一元一次方程的回归问题,也称作线性回归。
线性回归
线性回归是最简单的回归模型,非常适合用于发现事物之间的线性关系。
比如在下图所示的电路中,如果增加成倍电压,可以看到电流也会成倍增加。
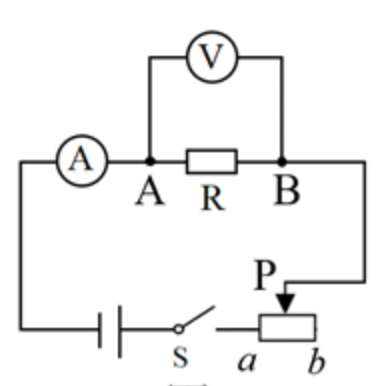
| 电压(V) | 电流(mA) |
|---|---|
| 5 | 5 |
| 10 | 10 |
| 20 | 20 |
通过观察测量结果,我们发现电压与电流的比总为一个常数,aka欧姆定律。
$$ V = IR $$其中,I为电流,V为电压,R为电阻。
如果仍然使用x、y、a字母来表示电流、电压和电阻的话,还可以写做:
$$ y=ax $$这是一个典型的一元一次方程,说明x和y之间(也就是电流和电压之间)存在着线性关系。

由于受测量方法和工具的限制,我们并不一定总能测得最精确的数据。随着测量次数的增加,会发现测量数据并不总是保持相同比例。
| 电压(V) | 电流(mA) |
|---|---|
| … | … |
| 2.5 | 2.8 |
| 5 | 4.6 |
| … | … |
将所有数据可视化到坐标系中,会发现无论如何都不可能找不到一条直线,将所有的点连起来。

我们相信这些数据点的偏差是由误差导致的,本质上电压和电流一定成线性关系,我们是否可以拨开遮挡真相的迷雾,找到那条本质的直线呢?
最小二乘法
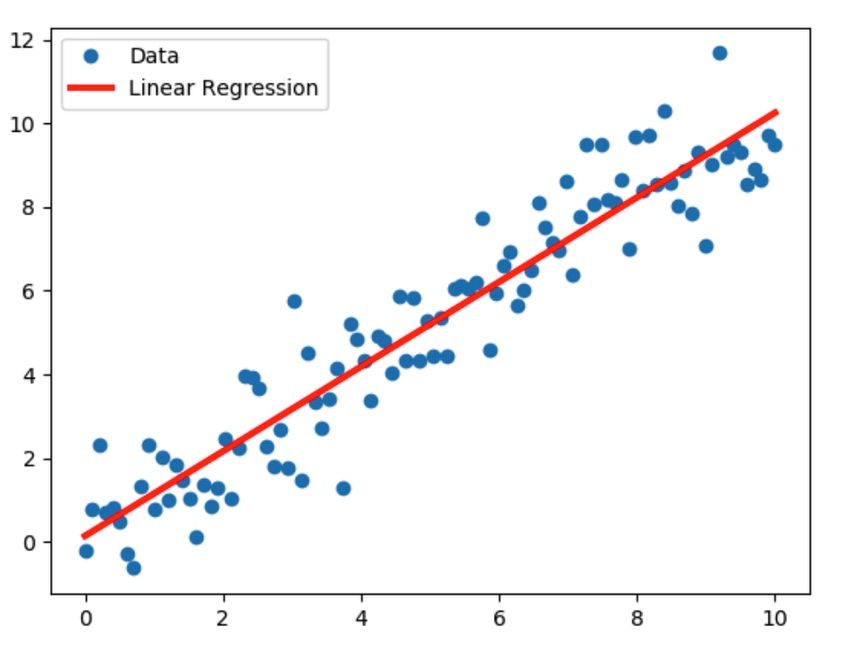
让我们尝试着调整参数a的取值,绘制出多条直线,如图所示。
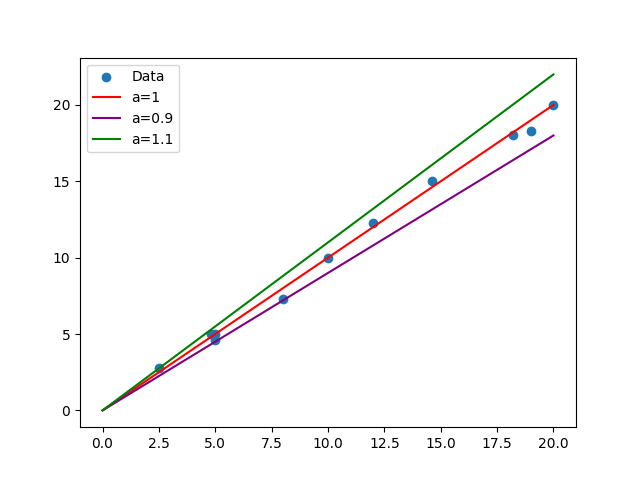
我们能直观的感受到,a=1的直线,相比a=0.9和a=1.1的直线更好,相对来说a=1更好的串联了这些数据点,尽管还有一些数据点“损失”掉了。
为了计算比较不同直线的优劣,我们定义一个函数来量化“损失”的大小,这就是损失函数!
损失函数是神经网络中最重要的概念之一,我们会在后面的文章中经常碰到它。最常用的一种损失函数是均方误差。
所谓误差,使指测量点到回归直线之间的距离(差值) $(ax_i - y_i)$ 。

考虑到这个距离(差值)有正有负,可以通过平方统一他们的符号,因为任何实数的平方都大于等于0。

然后$ \frac{\sum(各点的误差)^2}{n} $,即求误差平方和的平均值,以避免数字过大不方便后续运算。
我们要寻找的真相就是“使均方误差最小时的参数a的值”,因此这个方法被称作“最小二乘法”。
整体的公式如下:
$$ cost = \frac{\sum_{i=1}^n (ax_i - y_i)^2}{n} $$
求解最小二乘
如果对均方误差去括号化简,合并同类项,会得到一个形如这样的结果:
$$ cost = (\sum x^2)a^2 + (-\sum 2xy)a + \dots $$这说明,当测量数据确定的情况下,损失函数是一个关于a的二次函数,即抛物线。
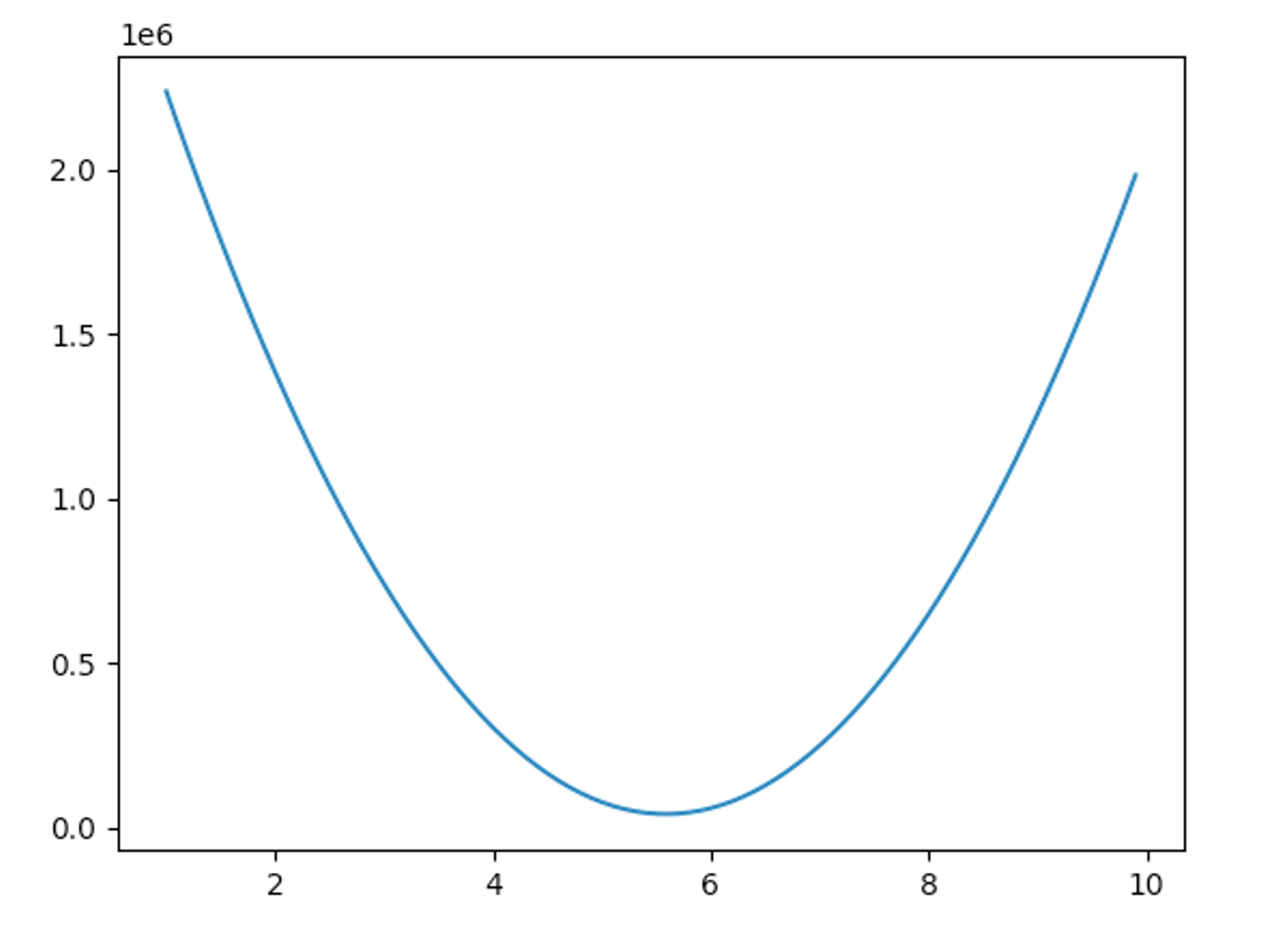
此外,$ a^2 $的系数是一些平方项的和,一定大于零,因此抛物线一定开口向上。因此,“使均方误差最小时的参数a的值”就是抛物线的顶点。
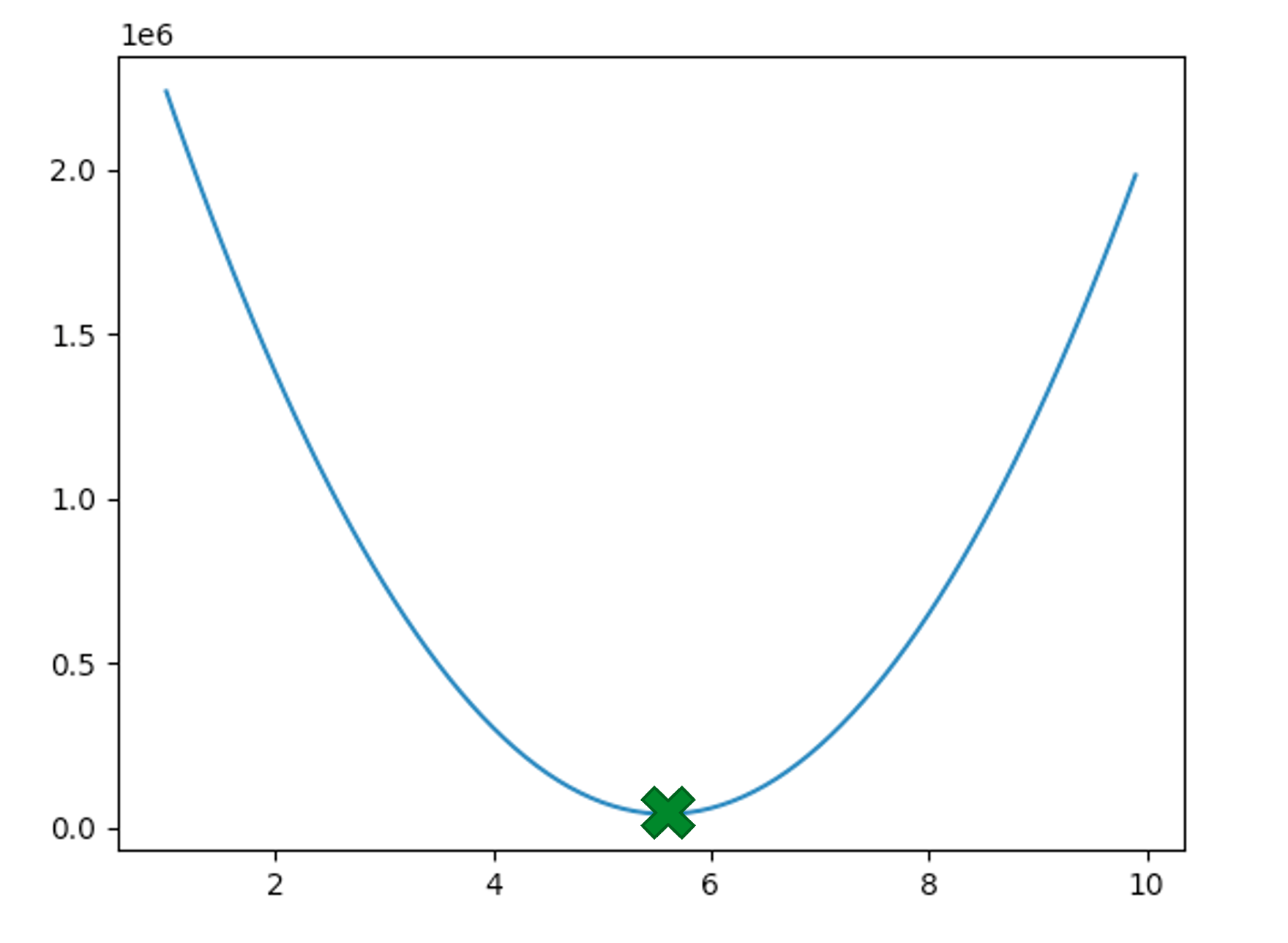
我们可以根据顶点坐标公式,快速的求得最优解。
$$ a_{min} = \frac{\sum xy}{\sum x^2} $$
在代码中引入了numpy库,以方便进行向量的运算:
import matplotlib.pyplot as plt
# 引入numpy方便进行向量运算
import numpy as np
# 测量数据转化为np格式
data = np.array([[5, 10, 20, 2.5, 5, 12, 8, 4.8, 18.2, 14.6, 19], [5, 10, 20, 2.8, 4.6, 12.3, 7.3, 5, 18, 15, 18.3 ]])
x = data[0]
y = data[1]
# 顶点坐标公式
a = np.sum(x * y) / np.sum(x ** 2)
print(a)
# 绘制散点图
plt.scatter(data[0], data[1], label="Data")
# 绘制直线图
plt.plot([0,20], [0,20*a], c='red', label=f"a={a}")
# 显示图例
plt.legend()
# 显示图像
plt.show()
我将本专栏所有的代码托管在gitee上了,你可以点击这个链接,或到gitee.com上搜索弦五 人工智能,查看和获取本课程的全部代码。
